Mathematiker des Monats März 2018
Christoph Gudermann (1798-1851)
überarbeitete Fassung anlässlich seines 170. Todestags am 25. September 2021
von
Peter Ullrich
Auch wenn Christoph Gudermann weder in Berlin studiert noch dort eine Stelle innegehabt hat,
sind seine Beziehungen zu dieser Stadt doch eng und vielfältig:
Er hat dort das Staatsexamen für das Lehramt an Gymnasien abgelegt,
er war einer der produktivsten Autoren von
August Leopold Crelles (1780–1855)
Journal
für die reine und angewandte Mathematik,
er wurde von der Philosophischen Fakultät der Berliner
Friedrich-Wilhelms-Universität
promoviert, und er war in der Mathematik formal gesehen der einzige akademische Lehrer von
Karl Weierstraß (1815–1897).
Leben
Geboren wurde Christoph Gudermann am 25. Mai 1798 in Vienenburg,
damals ein eigenständiger Ort im Bistum Hildesheim, seit 2014 ein Stadtteil von Goslar.
Im Zuge der Säkularisation kam die Gegend wenige Jahre später zum Königreich Hannover.
Christophs Vater Joseph war Lehrer in einem Nachbarort von Vienenburg;
von seiner Mutter Anna Maria ist nur der Geburtsname Eilers bekannt.
Für Christophs Lebensweg sollte von Bedeutung werden, dass er katholischer Konfession war.
In den Jahren 1809 bis 1820 besuchte er in Hildesheim das Gymnasium Josephinum.
Zunächst sollte er offenbar Geistlicher werden, wobei möglicherweise die soziale Versorgung
eine Rolle spielte: Als er sich am 13. April 1820 an der Universität in Göttingen einschrieb,
wurden ihm wegen Armut die Studiengebühren erlassen. Immatrikuliert wurde er jedoch
nicht für Theologie, sondern für Mathematik, auf die er sich von Anfang an spezialisierte.
Bereits im März 1822 legte Gudermann sein Staatsexamen für das Lehramt an Gymnasien ab –
und zwar in Berlin. Seine Gründe, das Königreich Hannover zu verlassen, sind nicht ganz klar:
Wie bereits erwähnt, war Vienenburg erst wenige Jahre zuvor zu diesem Königreich gekommen.
Vor allen Dingen aber hatten sich die Perspektiven für Gymnasiallehrer in Preußen durch
die Humboldtsche Bildungsreform erheblich verbessert.
Hinzu kam, dass Preußen nach dem Wiener Kongress mit den Provinzen Rheinland und Westfalen
große Gebiete mit überwiegend katholischer Bevölkerung hinzugewonnen hatte,
die für die Ausbildung der Gymnasiallehrer dort zuständigen Hochschulen in Bonn und
Münster ihren Betrieb aber erst 1818 (wieder)aufgenommen hatten.
Das Interesse des zuständigen preußischen Ministeriums an Gudermann war so groß,
dass er nach seinem Staatsexamen Geldzuwendungen erhielt, bis er im Oktober 1823 eine
Lehrerstelle in Cleve (seit 1935: Kleve) antrat. Dieses wurde seit 1614 von Brandenburg /
Preußen verwaltet, war jedoch aufgrund eines Religionsvergleichs katholisch geblieben.
In der Bibliothek der Schule, an die Gudermann kam, gab es allerdings kein einziges mathematisches
Buch. Seiner Bitte um Erhöhung des Bibliotheksetats wurde zwar Genüge getan,
jedoch mit der Auflage, „bei der Anschaffung von Büchern vorzüglich Philologie
und Geschichte im Auge“ zu haben.
Trotz dieser der Forschung nicht zuträglichen Lage zeigte Gudermann als Lehrer erstaunliche
mathematische Aktivität: So publizierte er seine erste Schrift bereits im Jahre 1825 und
schon 1830 ein Buch. 1829 hatte er weiterhin begonnen, in dem von Crelle herausgegebenen
Journal für die reine und angewandte Mathematik zu veröffentlichen,
wobei er es bis 1832 auf 11 publizierte Arbeiten brachte. Bei dieser Zählung wird wohlgemerkt
Gudermanns „Theorie der Potenzial- oder cyklisch-hyperbolischen Functionen“
als eine Arbeit gerechnet, obwohl der Separatabdruck ihrer zahlreichen Teile in Buchform
354 Druckseiten umfasst.
Die Humboldtsche Reform des Gymnasialwesens sah in Fällen wissenschaftlicher
Publikationstätigkeit von Gymnasiallehrern durchaus die Beförderung zum Oberlehrer vor.
Für Gudermann (wie auch für
Ernst Eduard Kummer (1810–1893) und
Weierstraß) war der Karriereschritt aber noch deutlicher:
Die Höhere Lehranstalt zu Münster war zwar keine Volluniversität,
sondern verfügte nur über eine (hier: Katholisch-)Theologische und
die Philosophische Fakultät und hatte zur Aufgabe, katholische Geistliche und Gymnasiallehrer
auszubilden. Im Jahr 1832 wurde sie zur Akademische[n] Lehranstalt mit Promotions- und
Habilitationsrecht nur für die Theologische Fakultät. 1834 wurde ihr Name erneut geändert,
jetzt in Königliche Theologische und Philosophische Akademie, und 1844 ihr wurde
auch für die Philosophische Fakultät das Promotionsrecht verliehen, allerdings mit Ausnahme
naturwissenschaftlicher Kandidaten. An diese Institution wurde Gudermann 1832 als Nachfolger des
überraschend verstorbenen Professors
Franz Baumann (1794–1832) der
Mathematik berufen.
Bevor er aber die außerordentliche Professur besetzen konnte, musste er noch promoviert
werden. Dazu wandte sich Gudermann nicht etwa an seine alte alma mater in Göttingen,
sondern an die Friedrich-Wilhelms-Universität in Berlin und bekundete dieser
gegenüber seine Bereitschaft, sich einem regulären Promotionsverfahren zu unterziehen.
Die zuständige Fakultät bat Crelle um eine Stellungnahme, der sich wie folgt zu Gudermann
und dessen Arbeiten äußerte:
„[Sie] zeichnen sich durch Klarheit, Gediegenheit, Schärfe der Begriffe und
Consequenz in der Ausführung auf eine höchst erstaunliche Weise aus.
[. . . ] Im Allgemeinen halte ich den Herrn Gudermann für einen mit ungewöhnlichem
Talent begabten und schon jetzt um seine Wissenschaft wesentlich verdienten Geometer.“
Dieses Gutachten reichte aus: Man beschloss, Gudermann die üblichen Regularien zu
erlassen, und promovierte ihn mit Datum vom 29. November 1832 ehrenhalber.
Crelles Wertschätzung für Gudermann war so hoch, dass er ihn 1835 auch für die
Nachfolge
Wilhelm Adolf Diesterwegs (1782–1835) an der Universität Bonn empfahl.
Berufen wurde stattdessen jedoch
Julius Plücker (1801–1868).
Gudermann dokumentierte seine Enttäuschung darüber, indem er in die Tageszeitungen von
Köln und Münster Anzeigen des Inhalts setzen ließ, man würde in den
preußischen Provinzen Rheinland und Westfalen demnächst nur bei ihm in Münster
Vorlesungen über moderne Mathematik hören können.
In der Tat:
Carl Gustav Jacob Jacobi (1804–1851) war im
Wintersemester 1829/30 weltweit der erste gewesen, der über elliptische Funktionen las;
Gudermann folgte ihm 1836 als zweiter nach. Auch publizierte er über dieses Thema,
etwa in den Jahren 1838 bis 1843 eine mehrteilige „Theorie der Modular-Functionen und der
Modular-Integrale“. Gemeint waren damit in der Tat elliptische Funktionen und elliptische
Integrale, die Gudermann unter anderem deshalb anders benannte, da diese nur am Rande etwas mit
Ellipsen zu tun haben. Angesichts dieser Aktivität ist es nicht überraschend, dass er
1838 zum ordentlichen Professor in Münster ernannt wurde.
Gudermann veröffentlichte insgesamt 41 Zeitschriftenartikel, allesamt im
Journal für die reine und angewandte Mathematik, und 3 Bücher
sowie 2 nochmals in Buchform separat abgedruckte Artikel.
Er verstarb in Münster am 25. September 1851 „durch einen Schlagfluß“,
nachdem er am Tag zuvor die Arbeit am zu Anfang auszugsweise reproduzierten Manuskript
abgeschlossen hatte.
Werk
Dass Gudermann in den Jahren 1820 bis 1822 in Göttingen Mathematik studierte,
hat einige Autoren dazu geführt, in ihm einen Gauß-Schüler zu sehen und
sogar zu behaupten, er habe bei diesem promoviert. Nun war aber Gauß seit 1807 Direktor
der Sternwarte und Professor für Astronomie und nicht für Mathematik.
Somit kündigte er insbesondere während der Studienzeit Gudermanns nur Vorlesungen zur
Astronomie an. Da dieser sich aber dezidiert für Mathematik und nicht für Astronomie
eingeschrieben hatte, hörte er seine Vorlesungen ordnungsgemäß bei dem
zuständigen Fachvertreter
Bernhard Friedrich Thibaut
(1775–1832).
Thibauts Mathematik basierte auf der kombinatorischen Analysis im Sinne von
Carl Friedrich
Hindenburg (1741–1808). Für ihn war die allgemeine
Arithmetik der wichtigste Teil der Mathematik; sie sollte gänzlich ohne geometrische
Betrachtungen behandelt werden. So unterstellte Thibaut etwa, dass sich alle Funktionen durch
Potenzreihen ausdrücken lassen, so dass es möglich ist, ihre Eigenschaften allein
durch Betrachtung ihrer Potenzreihenentwicklungen zu analysieren.
Als Besonderheit, die für den direkten Einfluss auf Gudermann (und damit den indirekten
auf Weierstraß) bedeutsam war, betrachtete Thibaut von Anfang an Potenzreihen komplexer
Argumente. Weiterhin hatte sich Thibaut der Geometrie zugewandt, die er als unabhängige
Teildisziplin der Mathematik betrachtete mit dem Dreieck als Grundform aller Anschauung.
Angesichts des genannten Hintergrundes der Thibautschen Mathematik ist es wenig überraschend,
dass das erste Manuskript Gudermanns, die 1825 erschienene Schrift „Allgemeiner Beweis des
polynomischen Lehrsatzes ohne die Voraussetzung des binomischen“, sich dem
polynomischen Lehrsatz widmete, den Hindenburg als „das wichtigste Theorem der
ganzen Analysis“ angesehen hatte (siehe [4]). Im gesamten mathematischen Werk Gudermanns machen
die Arbeiten zur kombinatorischen Analysis im engeren Sinne aber nur einen geringen Teil aus,
der zudem in die frühen Jahre seines Wirkens fällt.
Hingegen durchzieht die Beschäftigung mit der analytischen Sphärik im Sinne einer
analytischen Geometrie auf der Kugel seine gesamte Publikationstätigkeit, beginnend mit dem
1830 erschienenen Buch „Grundriss der analytischen Sphärik“ über das 1835
publizierte „Lehrbuch der niederen Sphärik“ bis hin zu posthum veröffentlichten
Artikeln. Gudermann wählte in seinen Arbeiten – von Thibaut abweichend –
einen rechnerisch-analytischen Zugang zur Geometrie und betrachtete zunächst simultan sowohl die
ebene als auch die sphärische Geometrie. Dabei stellte er fest, dass man die Formeln für die
ebene Geometrie jeweils als Spezialfall derer für die sphärische Geometrie interpretieren kann,
wenn man den Kugelradius nach Unendlich streben lässt. Dies führte ihn dazu,
nur sphärische Geometrie betreiben zu wollen, da diese die ebene als Grenzfall umfasst.
Fast zeitgleich mit den Arbeiten zur sphärischen Geometrie begann Gudermann,
über spezielle Typen analytischer Funktionen von komplexen Argumenten zu publizieren.
Gleich sein zweiter Artikel im Journal für die reine und angewandte Mathematik
trägt den Titel „Über die Potenzial-Functionen“. Den Terminus Potenzial
hatte Gudermann gewählt, weil sich die betrachteten Funktionen mit Hilfe von Potenzen definieren
lassen, genauer: der Exponential-Funktion, die hyperbolischen direkt, die trigonometrischen nach
Multiplikation des Arguments mit der imaginären Einheit. Indem er reelle und rein imaginäre
Argumente zuließ, gelang es Gudermann, die trigonometrischen und die hyperbolischen Funktionen
auf rein arithmetischer Basis in ein- und derselben Theorie gemeinsam zu behandeln.
Ganz in der Tradition der kombinatorischen Analysis waren dabei Potenzreihenentwicklungen ein
wichtiges Hilfsmittel. Der ausführlichen Darstellung dieser Theorie ist Gudermanns bereits
erwähnte Publikation „Theorie der Potenzial- oder cyklisch-hyperbolischen Functionen“
gewidmet, in deren erstem Teil sich auch die heute als Gudermannsche bezeichnete
Funktion findet.
Bald darauf verallgemeinerte er seine Betrachtungen: Hyperbolische und trigonometrische
Funktonen bzw. deren Umkehrfunktionen liefern Stammfunktionen für Integrale des
Typs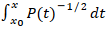 mit
P(t) ein Polynom vom Grad 1 oder 2
(ohne mehrfache Nullstellen), etwa
P(t) = 1 – t2. Ist hingegen
P(t) vom Grad 3 oder 4 (ohne mehrfache Nullstellen), etwa
P(t) = (1 – t2)(1 – k2t2),
so ergeben sich als Stammfunktionen bzw. deren Umkehrfunktionen Funktionen, welche Gudermann als
Modular-Functionen bezeichnete, da sie von dem Modulus genannten
Parameter k abhängen. Bereits damals wurden sie allerdings üblicherweise als
elliptische Funktionen bezeichnet.
mit
P(t) ein Polynom vom Grad 1 oder 2
(ohne mehrfache Nullstellen), etwa
P(t) = 1 – t2. Ist hingegen
P(t) vom Grad 3 oder 4 (ohne mehrfache Nullstellen), etwa
P(t) = (1 – t2)(1 – k2t2),
so ergeben sich als Stammfunktionen bzw. deren Umkehrfunktionen Funktionen, welche Gudermann als
Modular-Functionen bezeichnete, da sie von dem Modulus genannten
Parameter k abhängen. Bereits damals wurden sie allerdings üblicherweise als
elliptische Funktionen bezeichnet.
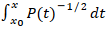 mit
P(t) ein Polynom vom Grad 1 oder 2
(ohne mehrfache Nullstellen), etwa
P(t) = 1 – t2. Ist hingegen
P(t) vom Grad 3 oder 4 (ohne mehrfache Nullstellen), etwa
P(t) = (1 – t2)(1 – k2t2),
so ergeben sich als Stammfunktionen bzw. deren Umkehrfunktionen Funktionen, welche Gudermann als
Modular-Functionen bezeichnete, da sie von dem Modulus genannten
Parameter k abhängen. Bereits damals wurden sie allerdings üblicherweise als
elliptische Funktionen bezeichnet.
mit
P(t) ein Polynom vom Grad 1 oder 2
(ohne mehrfache Nullstellen), etwa
P(t) = 1 – t2. Ist hingegen
P(t) vom Grad 3 oder 4 (ohne mehrfache Nullstellen), etwa
P(t) = (1 – t2)(1 – k2t2),
so ergeben sich als Stammfunktionen bzw. deren Umkehrfunktionen Funktionen, welche Gudermann als
Modular-Functionen bezeichnete, da sie von dem Modulus genannten
Parameter k abhängen. Bereits damals wurden sie allerdings üblicherweise als
elliptische Funktionen bezeichnet.
Um 1835 herum begann Gudermann mit Publikationen über diesen damals ganz neuen Funktionstyp
und verfasste bald auch seine bereits erwähnte „Theorie der Modular-Functionen und der
Modular-Integrale“. Angesichts der Nähe der Modular-Functionen zu den
zuvor betrachteten Potenzial-Functionen überrascht es nicht, dass er dabei
vergleichbare Methoden zur Untersuchung verwendete. Insbesondere Entwicklungen in Reihen waren ein
zentrales Instrument und wurden – in teilweise erschreckender Ausführlichkeit –
explizit angegeben.
Dabei war Gudermann durchaus auch daran interessiert, numerisch schnell konvergente Reihen zu erhalten.
In diesem Zusammenhang konstatierte er 1838:
„Es ist ein bemerkenswerther
Umstand, daß sowohl die unendlichen Producte in § 58, als auch die so eben gefundenen Reihen
einen im Ganzen gleichen Grad der Convergenz haben.“
Auch, wenn er diese Bemerkung nicht weiter diskutierte, hat sie ihm doch einen Platz in der
Ahnengalerie der gleichmäßigen Konvergenz gesichert.
1838 kam Weierstraß zum Mathematik-Studium nach Münster, um Gymnasiallehrer zu werden.
Er hörte im Wintersemester 1838/39 und im Sommersemester 1839 Vorlesungen bei Gudermann,
nachdem er bereits während seines Kameralistik-Studiums in Bonn die Mitschrift einer von
dessen Vorlesungen studiert hatte. Über das Verhältnis zwischen Gudermann und ihm ist
bereits zu Lebzeiten von Weierstraß vieles geschrieben worden, was auch später noch
unkritisch übernommen wurde. Neuere Arbeiten belegen hingegen zum Beispiel, dass Weierstraß
sein Staatsexamen in Münster nur aufgrund einer Sondergenehmigung bestanden hatte,
dass er danach durchaus Kontakte mit der akademischen Welt suchte und dass Gudermann das nur ein Jahr
nach dem Weggang von Weierstraß Münster verliehene Promotionsrecht umgehend nutzte,
wenn auch nicht mit diesem als Doktorschüler. In seiner „Akademischen Antrittsrede“
vor der
Königlich-Preußischen Akademie
der Wissenschaften zu Berlin jedenfalls berichtete
Weierstraß über Gudermanns Einfluss auf seine Entwicklung:
„[D]ie Theorie der
elliptischen Functionen, hatte von der Zeit an, wo ich unter der Leitung meines hochverehrten
Lehrers G u d e r m a n n , dem ich stets eine
dankbare Erinnerung bewahren werde, die erste Bekanntschaft mit derselben machte,
eine mächtige Anziehungskraft auf mich geübt.“
Widersprüchliche Angaben zu den Lebensdaten von Gudermann
Nicht nur im Internet, sondern auch in gedruckten, allgemein als zuverlässig geltenden
Referenzwerken werden die Lebensdaten Gudermanns bisweilen falsch angegeben, beginnend
vom Datum seines Geburtstags über die räumliche Lage seines Geburtsorts bis
hin zu seinem Sterbetag, sogar seinem Sterbejahr: Neben der korrekten Zahl 1851 findet
sich auch die Angabe 1852, sogar simultan in ein und demselben Artikel. Gerade das
Sterbejahr lässt sich aber leicht klären, da bereits in dem 1851 erschienenen Band 42 des
Journal[s] für die reine und angewandte Mathematik eine Würdigung Gudermanns durch
Crelle erschien.
Leben und Werk Gudermanns haben in den letzten Jahren verstärktes Interesse gefunden.
Die daraus entstandenen, teilweise von einander unabhängigen Untersuchungen haben zu einer
Klärung dieser Widersprüche geführt. Besonders hinzuweisen ist auf die Masterarbeit von
Frau Blauth [1], die nicht nur Gudermanns Beitrag zur niederen Sphärik analysiert,
sondern auch zahlreiche seiner Lebensdaten durch Archivstudien belegt hat. In noch bestehenden
Zweifelsfällen wurden daher diese Angaben verwendet.
Weiterführende Literatur
| [1] | Anne Blauth: Christoph Gudermann und sein „Lehrbuch der niederen Sphärik“, Masterarbeit, Münster, 2020 | |
| [2] | Jürgen Elstrodt: Die prägenden Jahre im Leben von Karl Weierstraß, In Wolfgang König, Jürgen Sprekels (Hrsg.): Karl Weierstraß (1815–1897), Aspekte seines Lebens und Werkes – Aspects of his Life and Work, Springer Spektrum, Wiesbaden, 2015, S. 11 - 51 | |
| [3] | Rudolf Fritsch: Gudermann, Bodenmiller und der Satz von Bodenmiller-Steiner, Didaktik der Mathematik 20, Heft 3 (1992), 165 - 187 | |
| [4] | Carl Friedrich Hindenburg: Der polynomische Lehrsatz das wichtigste Theorem der ganzen Analysis nebst einigen verwandten und andern Sätzen, gedruckt bei Gerhard Fleischer dem Jüngeren, Leipzig, 1796 | |
| [5] | Gert Schubring: Warum Karl WEIERSTRASS beinahe in der Lehrerprüfung gescheitert wäre, Der Mathematikunterricht 35, Heft 1 (1989), 13 - 29 | |
| [6] | Peter Ullrich: Karl Weierstraß und die erste Promotion in Mathematik an der Akademie zu Münster, In Gudrun Wolfschmidt (Hrsg.): Es gibt für Könige keinen besonderen Weg zur Geometrie, Festschrift für Karin Reich, Algorismus 60 (2007), Dr. Erwin Rauner Verlag, Augsburg, S. 145 - 162 | |
| [7] | Peter Ullrich: Christoph Gudermann (1798-1851) – nicht nur der akademische Lehrer von Weierstraß, Vortrag am 26. Mai 2017 in Wittenberg auf der Tagung der Fachgruppe „Geschichte der Mathematik“ der DMV und des Arbeitskreises „Mathematikgeschichte und Unterricht“ der GDM, erscheint in deren Tagungsband |
Bildnachweis
| Schriftfragment | Der Beginn der letzten Zeilen mathematischen Inhalts von Gudermanns Hand, reproduziert im Journal für die reine und angewandte Mathematik Band 43, S. 375 |
